Words as Vectors

[This post was originally published on April 13, 2015.]

Vector space model is well known in information retrieval where each document is represented as a vector. The vector components represent weights or importance of each word in the document. The similarity between two documents is computed using the cosine similarity measure.

Although the idea of using vector representation for words also has been around for some time, the interest in word embedding, techniques that map words to vectors, has been soaring recently. One driver for this has been Tomáš Mikolov's Word2vec algorithm which uses a large amount of text to create high-dimensional (50 to 300 dimensional) representations of words capturing relationships between words unaided by external annotations. Such representation seems to capture many linguistic regularities. For example, it yields a vector approximating the representation for vec('Rome') as a result of the vector operation vec('Paris') - vec('France') + vec('Italy').

Word2vec uses a single hidden layer, fully connected neural network as shown below. The neurons in the hidden layer are all linear neurons. The input layer is set to have as many neurons as there are words in the vocabulary for training. The hidden layer size is set to the dimensionality of the resulting word vectors. The size of the output layer is same as the input layer. Thus, assuming that the vocabulary for learning word vectors consists of V words and N to be the dimension of word vectors, the input to hidden layer connections can be represented by matrix WI of size VxN with each row representing a vocabulary word. In same way, the connections from hidden layer to output layer can be described by matrix WO of size NxV. In this case, each column of WO matrix represents a word from the given vocabulary. The input to the network is encoded using "1-out of -V" representation meaning that only one input line is set to one and rest of the input lines are set to zero.

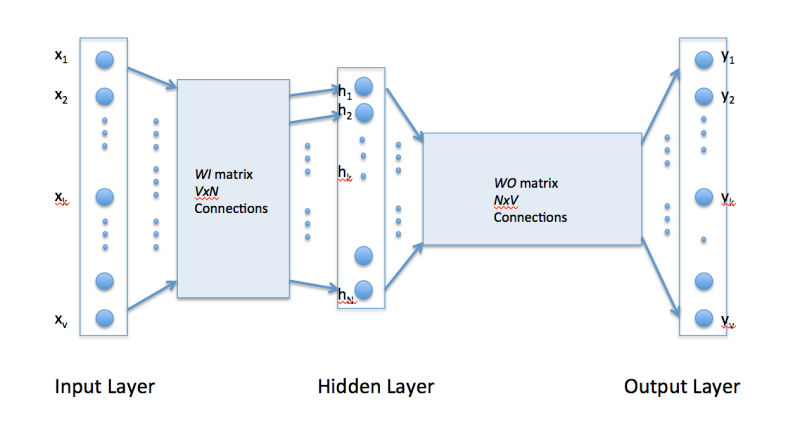
To get a better handle on how Word2vec works, consider the training corpus having the following sentences:

"the dog saw a cat", "the dog chased the cat", "the cat climbed a tree"

The corpus vocabulary has eight words. Once ordered alphabetically, each word can be referenced by its index. For this example, our neural network will have eight input neurons and eight output neurons. Let us assume that we decide to use three neurons in the hidden layer. This means that WI and WO will be 8x3 and 3x8 matrices, respectively. Before training begins, these matrices are initialized to small random values as is usual in neural network training. Just for the illustration sake, let us assume WI and WO to be initialized to the following values:

WI =

W0 =

Suppose we want the network to learn relationship between the words "cat" and "climbed". That is, the network should show a high probability for "climbed" when "cat" is inputted to the network. In word embedding terminology, the word "cat" is referred as the context word and the word "climbed" is referred as the target word. In this case, the input vector X will be [0 1 0 0 0 0 0 0]t. Notice that only the second component of the vector is 1. This is because the input word is "cat" which is holding number two position in sorted list of corpus words. Given that the target word is "climbed", the target vector will look like [0 0 0 1 0 0 0 0 ]t.

With the input vector representing "cat", the output at the hidden layer neurons can be computed as

Ht = XtWI = [-0.490796 -0.229903 0.065460]

It should not surprise us that the vector H of hidden neuron outputs mimics the weights of the second row of WI matrix because of 1-out-of-V representation. So the function of the input to hidden layer connections is basically to copy the input word vector to hidden layer. Carrying out similar manipulations for hidden to output layer, the activation vector for output layer neurons can be written as

HtWO = [0.100934 -0.309331 -0.122361 -0.151399 0.143463 -0.051262 -0.079686 0.112928]

Since the goal is produce probabilities for words in the output layer, Pr(wordk|wordcontext) for k = 1, V, to reflect their next word relationship with the context word at input, we need the sum of neuron outputs in the output layer to add to one. Word2vec achieves this by converting activation values of output layer neurons to probabilities using the softmax function. Thus, the output of the k-th neuron is computed by the following expression where activation(n) represents the activation value of the n-th output layer neuron:

Thus, the probabilities for eight words in the corpus are:

0.143073 0.094925 0.114441 0.111166 0.149289 0.122874 0.119431 0.144800

The probability in bold is for the chosen target word "climbed". Given the target vector [0 0 0 1 0 0 0 0 ]t, the error vector for the output layer is easily computed by subtracting the probability vector from the target vector. Once the error is known, the weights in the matrices WO and WI

The probability in bold is for the chosen target word "climbed". Given the target vector [0 0 0 1 0 0 0 0 ]t, the error vector for the output layer is easily computed by subtracting the probability vector from the target vector. Once the error is known, the weights in the matrices WO and WI

can be updated using backpropagation. Thus, the training can proceed by presenting different context-target words pair from the corpus. In essence, this is how Word2vec learns relationships between words and in the process develops vector representations for words in the corpus.

Continuous Bag of Words (CBOW) Learning

The above description and architecture is meant for learning relationships between pair of words. In the continuous bag of words model, context is represented by multiple words for a given target words. For example, we could use "cat" and "tree" as context words for "climbed" as the target word. This calls for a modification to the neural network architecture. The modification, shown below, consists of replicating the input to hidden layer connections C times, the number of context words, and adding a divide by C operation in the hidden layer neurons. [An alert reader pointed that the figure below might lead some readers to think that CBOW learning uses several input matrices. It is not so. It is the same matrix, WI, that is receiving multiple input vectors representing different context words]

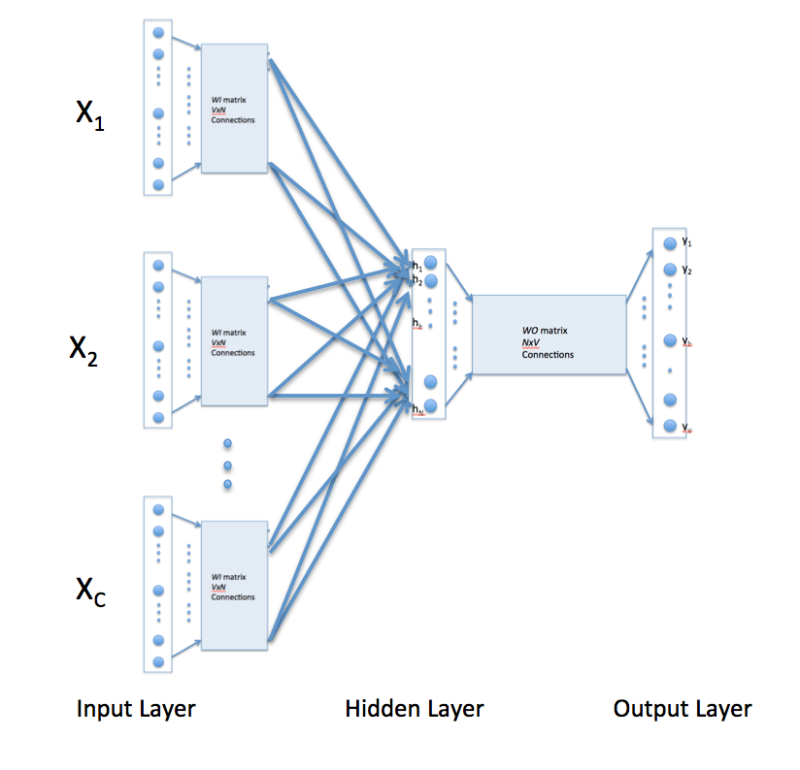
With the above configuration to specify C context words, each word being coded using 1-out-of-V representation means that the hidden layer output is the average of word vectors corresponding to context words at input. The output layer remains the same and the training is done in the manner discussed above.

Skip-Gram Model

Skip-gram model reverses the use of target and context words. In this case, the target word is fed at the input, the hidden layer remains the same, and the output layer of the neural network is replicated multiple times to accommodate the chosen number of context words. Taking the example of "cat" and "tree" as context words and "climbed" as the target word, the input vector in the skim-gram model would be [0 0 0 1 0 0 0 0 ]t, while the two output layers would have [0 1 0 0 0 0 0 0] t and [0 0 0 0 0 0 0 1 ]t as target vectors respectively. In place of producing one vector of probabilities, two such vectors would be produced for the current example. The error vector for each output layer is produced in the manner as discussed above. However, the error vectors from all output layers are summed up to adjust the weights via backpropagation. This ensures that weight matrix WO for each output layer remains identical all through training.

In above, I have tried to present a simplistic view of Word2vec. In practice, there are many other details that are important to achieve training in a reasonable amount of time. At this point, one may ask the following questions:

1. Are there other methods for generating vector representations of words? The answer is yes and I will be describing another method in my next post.

2. What are some of the uses/advantages of words as vectors. Again, I plan to answer it soon in my coming posts.

Embeddings Beyond Words: Intro to Sentence Embeddings

It wouldn't be an exaggeration to say that the recent advances in Natural Language Processing (NLP) technology can be, to a large extent, attributed to the use of very high-dimensional vectors for language representation. These high-dimensional, 764 dimensions is common, vector representations are called embeddings and are aimed at capturing semantic meaning and relationships between linguistic items.

Although the idea of using vector representation for words has been around for many years, the interest in word embedding took a quantum jump with Tomáš Mikolov’s Word2vec algorithm in 2013. Since then, many methods for generating word embeddings, for example GloVe and BERT, have been developed. Before moving on further, let's see briefly how word embedding methods work.

Word Embedding: How is it Performed?

I am going to explain how word embedding is done using the Word2vec method. This method uses a linear encoder-decoder network with a single hidden layer. The input layer of the encoder is set to have as many neurons as there are words in the vocabulary for training. The hidden layer size is set to the dimensionality of the resulting word vectors. The size of the output layer is same as the input layer. The input words to the encoder are encoded using one-hot vector encoding where the size of the vector corresponds to the vocabulary. The figure below shows the arrangement for learning embeddings.

The embeddings are learned by adjusting weights so that for a target word, say fox in a piece of text "The quick brown fox jumped over the fence", the probability for the designated context word, say jumped is high. There are two major variations to this basic technique. In a variation known as the continuous bag of words (CBW), multiple context words are used. Thus, the system may use brown, jumped and fence as the context words. In another scheme, known as the skip-gram model, the use of target and context words is reversed. Thus, the target word is fed on the input side and the weights are modified to increase probabilities for the prediction of context words. In both of these cases, the above architecture needs modification. You can read details about the architecture changes as well as look at a simple example in the blog post that I did a while ago.

Sentence Embeddings

While word embeddings are useful, we are often working with text to perform tasks such as text classification, sentiment analysis, and topic detection etc. Thus, it would be logical to extend the idea of word embeddings to sentences.  One simple way to accomplish this is to take the average of embeddings of different words in a sentence. However, such an approach doesn't take into account the word order and thus results in vectors that aren't very good at capturing the sentence meaning. Instead, the sentence embeddings are obtained by using transformer models such BERT (Bidirectional Encoder Representations from Transformers) which make use of attention mechanism to gauge the importance of different words in a sentence. BERT outputs for each token in the given input text its contextualized embedding. In order to create a fixed-sized sentence embedding out of this, the model applies mean pooling, i.e., the output embeddings for all tokens are pooled to yield a fixed-sized vector. The Sentence-BERT or simply SBERT is a package that you can use to create sentence embeddings without worrying about pooling. 

One issue facing BERT/SBERT is that of encountering an out of vocabulary word, that is a word that wasn't part of the text corpus used to train BERT. In such a case, an embedding for such a word doesn't exist. BERT/SBERT solve this by using a WordPiece tokenizer which breaks every word into one or more tokens. As an example, the word snowboarding will be tokenized through three tokens: snow, board, ing. This ensures embedding being created for any new word. SBERT permits creating a single vector embedding for sequences containing no more than 128 tokens. Sequence tokens beyond 128 are simply discarded.

Sentence Embedding Libraries

Other than SBERT, there are many libraries that one can use. Some of these are:

• TensorFlow Hub - Provides pre-trained encoders like BERT and other transformer models. Makes it easy to generate sentence embeddings.

• InferSent - Facebook AI research model for sentence embeddings trained on natural language inference data.

• Universal Sentence Encoder (USE) - Google model trained on a variety of data sources to generate general purpose sentence embeddings.

• Flair - NLP library with models like Flair embeddings trained on unlabeled data which can provide sentence representations.

• Doc2Vec - Extension of Word2Vec that can learn embeddings for sentences and documents.

• Stanford SkipThoughts - Unupervised model trained to predict surrounding sentences based on context.

• GenSim - Includes implementations of models like Doc2Vec for generating sentence and paragraph embeddings.

• SentenceTransformers - Library for state-of-the-art sentence embeddings based on transformers. Includes pretrained models like BERT and RoBERTa.

The choice of model depends on your use case. For general purposes, pretrained universal encoders like USE and SBERT provide robust sentence vectors. For domain-specific tasks, fine-tuning transformer models like BERT often produces the best performance.

One word of caution while using embeddings. Never mix embeddings generated by two different libraries. Embeddings produced via each method/framework are unique to that method and the training corpus.

An Example of Sentence Embedding for Measuring Similarity

Let's take a look at using sentence embedding to capture semantic similarity between pairs of sentences. We will use SBERT for this purpose. First, we install and import the necessary libraries and decide upon the sentence transformer model to be used.

! pip install sentence-transformers




from sentence_transformers import SentenceTransformer

model = SentenceTransformer('all-mpnet-base-v2')

Next, we specify the sentences that we are using.

sentences = [

"The sky is blue and beautiful",

"Love this blue and beautiful sky!",

"The brown fox is quick and the blue dog is lazy!",

"The dog is lazy but the brown fox is quick!",

"the bees decided to have a mutiny against their queen",

"the sign said there was road work ahead so she decided to speed up",

"on a scale of one to ten, what's your favorite flavor of color?",

"flying stinging insects rebelled in opposition to the matriarch"

]

embeddings = model.encode(sentences)

embeddings.shape

(8, 768)

So, the embedding results in eight vectors of 768 dimensions. Next, we import a utility from sentence transformer library and compute cosine similarities between different pairs. Remember, the cosine similarity value close to one indicates very high degree of similarity and low values are indicative of almost no similarity.

from sentence_transformers import util
#Compute cosine similarity between all pairs
cos_sim = util.cos_sim(embeddings, embeddings)
print(cos_sim)

tensor([[ 1.0000, 0.7390, 0.2219, 0.1689, 0.1008, 0.1191, 0.2174, 0.0628], [ 0.7390, 1.0000, 0.1614, 0.1152, 0.0218, 0.0713, 0.2854, -0.0181], [ 0.2219, 0.1614, 1.0000, 0.9254, 0.1245, 0.2171, 0.1068, 0.0962], [ 0.1689, 0.1152, 0.9254, 1.0000, 0.1018, 0.2463, 0.0463, 0.0706], [ 0.1008, 0.0218, 0.1245, 0.1018, 1.0000, 0.2005, 0.0153, 0.6084], [ 0.1191, 0.0713, 0.2171, 0.2463, 0.2005, 1.0000, 0.0116, 0.1011], [ 0.2174, 0.2854, 0.1068, 0.0463, 0.0153, 0.0116, 1.0000, -0.0492], [ 0.0628, -0.0181, 0.0962, 0.0706, 0.6084, 0.1011, -0.0492, 1.0000]])

Looking at the resulting similarity values, we see that the sentence#1 and sentence#2 pair has a high degree of similarity. Sentence#3 and sentence#4 also generate a very high value of cosine similarity. Interestingly, sentence#5 and sentence#8 are also deemed to have a good semantic similarity, although they do not share any descriptive words. Thus, the sentence embedding is doing a pretty good job of capturing sentence semantics.

Comparison with TF-IDF Vectorization

Information Retrieval (IR) community for a long time has been representing text as vectors for matching documents. The approach, known as the bag-of-words model, uses a set of words or terms to characterize text.  Each word or term is assigned a weight following the  TF-IDF weighting scheme. In this scheme, the weight assigned to a word is based upon: (i) how often it appears in the document being vectorized, the term frequency (TF) component of the weighting scheme, and (ii) how rare is the word in the entire document collection, the inverse document frequency (IDF) component of the weighting scheme. The vector size is governed by the number of terms used from the entire document collection, i.e. the vocabulary size. You can read details about TF-IDF vectorization in this blog post.

Let's see how well the TF-IDF vectorization captures similarities between document in comparison with the sentence embedding. We will use the same set of sentences to perform vectorization and similarity calculations as shown below.

from sklearn.feature_extraction.text import TfidfVectorizer

from sklearn.metrics.pairwise import cosine_similarity

vectorizer = TfidfVectorizer(ngram_range = (1,2),stop_words='english')

tfidf = vectorizer.fit_transform(sentences)

similarity =cosine_similarity(tfidf,tfidf)

np.set_printoptions(precision=4)

print(similarity)

[[1. 0.5818 0.0962 0. 0. 0. 0. 0. ] [0.5818 1. 0.0772 0. 0. 0. 0. 0. ] [0.0962 0.0772 1. 0.7654 0. 0. 0. 0. ] [0. 0. 0.7654 1. 0. 0. 0. 0. ] [0. 0. 0. 0. 1. 0.0761 0. 0. ] [0. 0. 0. 0. 0.0761 1. 0. 0. ] [0. 0. 0. 0. 0. 0. 1. 0. ] [0. 0. 0. 0. 0. 0. 0. 1. ]]

Looking at the above results, we see that TF-IDF vectorization is unable to determine similarity between 
sentence#5 and sentence#8 which the sentence embedding was able to pick up despite of the absence of the common descriptive words in the sentence pair.

Thus, TF-IDF vectorizer is good as long as there are shared descriptive words. But the sentence embedding is able to capture semantic similarities without even shared descriptive words. This is possible because the high-dimensional embedded vectors learn relationships between different words and their context during training and utilize those relationships during similarity computation as well as for other NLP tasks.

Now you might be wondering whether the embedding concept can be applied to images and graphs. The answer is yes and I hope to dwell on these in my future posts.