[This post was originally published on April 13, 2015.]
Vector space model is well known in information retrieval where each document is represented as a vector. The vector components represent weights or importance of each word in the document. The similarity between two documents is computed using the cosine similarity measure.
Although the idea of using vector representation for words also has been around for some time, the interest in word embedding, techniques that map words to vectors, has been soaring recently. One driver for this has been Tomáš Mikolov's Word2vec algorithm which uses a large amount of text to create high-dimensional (50 to 300 dimensional) representations of words capturing relationships between words unaided by external annotations. Such representation seems to capture many linguistic regularities. For example, it yields a vector approximating the representation for vec('Rome') as a result of the vector operation vec('Paris') - vec('France') + vec('Italy').
Word2vec uses a single hidden layer, fully connected neural network as shown below. The neurons in the hidden layer are all linear neurons. The input layer is set to have as many neurons as there are words in the vocabulary for training. The hidden layer size is set to the dimensionality of the resulting word vectors. The size of the output layer is same as the input layer. Thus, assuming that the vocabulary for learning word vectors consists of V words and N to be the dimension of word vectors, the input to hidden layer connections can be represented by matrix WI of size VxN with each row representing a vocabulary word. In same way, the connections from hidden layer to output layer can be described by matrix WO of size NxV. In this case, each column of WO matrix represents a word from the given vocabulary. The input to the network is encoded using "1-out of -V" representation meaning that only one input line is set to one and rest of the input lines are set to zero.
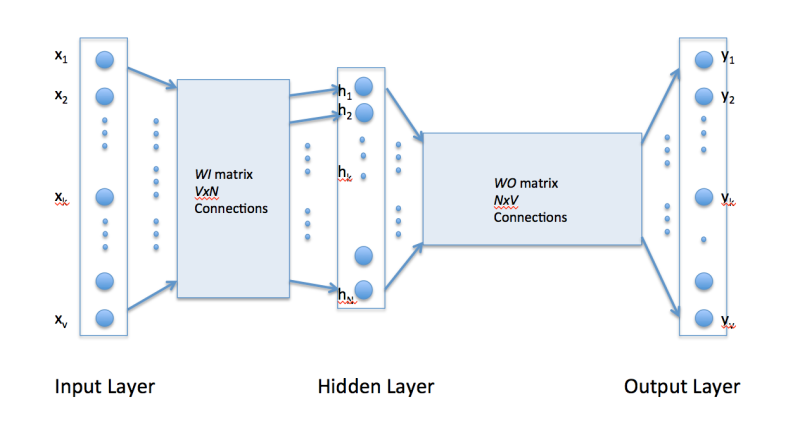
To get a better handle on how Word2vec works, consider the training corpus having the following sentences:
"the dog saw a cat", "the dog chased the cat", "the cat climbed a tree"
The corpus vocabulary has eight words. Once ordered alphabetically, each word can be referenced by its index. For this example, our neural network will have eight input neurons and eight output neurons. Let us assume that we decide to use three neurons in the hidden layer. This means that WI and WO will be 8x3 and 3x8 matrices, respectively. Before training begins, these matrices are initialized to small random values as is usual in neural network training. Just for the illustration sake, let us assume WI and WO to be initialized to the following values:
WI =

W0 =

Suppose we want the network to learn relationship between the words "cat" and "climbed". That is, the network should show a high probability for "climbed" when "cat" is inputted to the network. In word embedding terminology, the word "cat" is referred as the context word and the word "climbed" is referred as the target word. In this case, the input vector X will be [0 1 0 0 0 0 0 0]t. Notice that only the second component of the vector is 1. This is because the input word is "cat" which is holding number two position in sorted list of corpus words. Given that the target word is "climbed", the target vector will look like [0 0 0 1 0 0 0 0 ]t.
With the input vector representing "cat", the output at the hidden layer neurons can be computed as
Ht = XtWI = [-0.490796 -0.229903 0.065460]It should not surprise us that the vector H of hidden neuron outputs mimics the weights of the second row of WI matrix because of 1-out-of-V representation. So the function of the input to hidden layer connections is basically to copy the input word vector to hidden layer. Carrying out similar manipulations for hidden to output layer, the activation vector for output layer neurons can be written as
HtWO = [0.100934 -0.309331 -0.122361 -0.151399 0.143463 -0.051262 -0.079686 0.112928]Since the goal is produce probabilities for words in the output layer, Pr(wordk|wordcontext) for k = 1, V, to reflect their next word relationship with the context word at input, we need the sum of neuron outputs in the output layer to add to one. Word2vec achieves this by converting activation values of output layer neurons to probabilities using the softmax function. Thus, the output of the k-th neuron is computed by the following expression where activation(n) represents the activation value of the n-th output layer neuron:

Thus, the probabilities for eight words in the corpus are:
0.143073 0.094925 0.114441 0.111166 0.149289 0.122874 0.119431 0.144800
The probability in bold is for the chosen target word "climbed". Given the target vector [0 0 0 1 0 0 0 0 ]t, the error vector for the output layer is easily computed by subtracting the probability vector from the target vector. Once the error is known, the weights in the matrices WO and WI
The probability in bold is for the chosen target word "climbed". Given the target vector [0 0 0 1 0 0 0 0 ]t, the error vector for the output layer is easily computed by subtracting the probability vector from the target vector. Once the error is known, the weights in the matrices WO and WI
can be updated using backpropagation. Thus, the training can proceed by presenting different context-target words pair from the corpus. In essence, this is how Word2vec learns relationships between words and in the process develops vector representations for words in the corpus.
Continuous Bag of Words (CBOW) Learning
The above description and architecture is meant for learning relationships between pair of words. In the continuous bag of words model, context is represented by multiple words for a given target words. For example, we could use "cat" and "tree" as context words for "climbed" as the target word. This calls for a modification to the neural network architecture. The modification, shown below, consists of replicating the input to hidden layer connections C times, the number of context words, and adding a divide by C operation in the hidden layer neurons. [An alert reader pointed that the figure below might lead some readers to think that CBOW learning uses several input matrices. It is not so. It is the same matrix, WI, that is receiving multiple input vectors representing different context words]
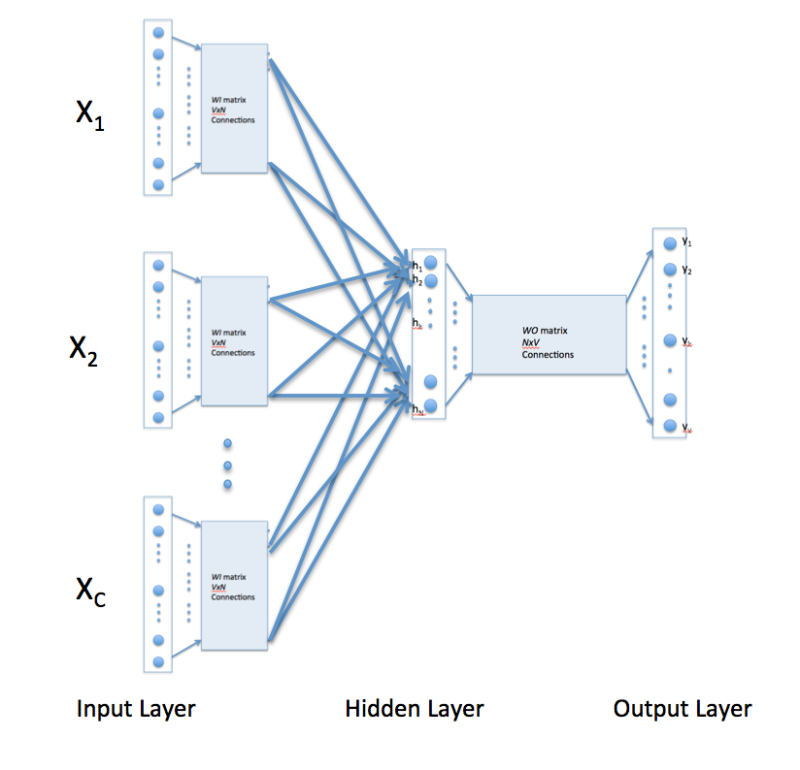
With the above configuration to specify C context words, each word being coded using 1-out-of-V representation means that the hidden layer output is the average of word vectors corresponding to context words at input. The output layer remains the same and the training is done in the manner discussed above.
Skip-Gram Model
Skip-gram model reverses the use of target and context words. In this case, the target word is fed at the input, the hidden layer remains the same, and the output layer of the neural network is replicated multiple times to accommodate the chosen number of context words. Taking the example of "cat" and "tree" as context words and "climbed" as the target word, the input vector in the skim-gram model would be [0 0 0 1 0 0 0 0 ]t, while the two output layers would have [0 1 0 0 0 0 0 0] t and [0 0 0 0 0 0 0 1 ]t as target vectors respectively. In place of producing one vector of probabilities, two such vectors would be produced for the current example. The error vector for each output layer is produced in the manner as discussed above. However, the error vectors from all output layers are summed up to adjust the weights via backpropagation. This ensures that weight matrix WO for each output layer remains identical all through training.
In above, I have tried to present a simplistic view of Word2vec. In practice, there are many other details that are important to achieve training in a reasonable amount of time. At this point, one may ask the following questions:
1. Are there other methods for generating vector representations of words? The answer is yes and I will be describing another method in my next post.
2. What are some of the uses/advantages of words as vectors. Again, I plan to answer it soon in my coming posts.
